1. 전제조건
- 제품의 부품을 보관하는 창고에서 공장까지 운송 비용을 낮추기
- 어떤 창고에서 어떤 공장으로 어느 정도의 양을 운송할 지 검토
2. 데이터 정보
- trans_route.csv : 운송 정보 - 공장에서 창고까지 얼마나 운송했는지
- trans_route_pos.csv : 노드 좌표
- trans_cost.csv : 각 경로에 필요한 비용
- demand.csv : 공장 수요량
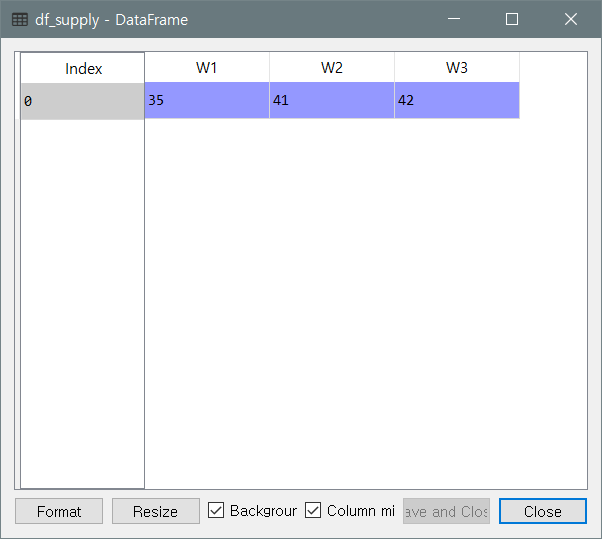
- supply.csv : 창고 공급량
- trans_route_new.csv : trans_route에서 변경된 데이터 (W1에서 F4 운송을 줄이고, W2에서 F4로 운송 보충)
import os
import pandas as pd
import numpy as np
import networkx as nx
import matplotlib.pyplot as plt
os.chdir('C:\\Users\\leeso\\Downloads\\pyda100-master\\6장')
df_tr = pd.read_csv('trans_route.csv',index_col='공장')
df_pos = pd.read_csv('trans_route_pos.csv')
df_tc = pd.read_csv('trans_cost.csv',index_col='공장')
df_tr = pd.read_csv('trans_route.csv', index_col="공장")
df_demand = pd.read_csv('demand.csv')
df_supply = pd.read_csv('supply.csv')
df_tr_new = pd.read_csv('trans_route_new.csv',index_col='공장')




3. NetworkX 라이브러리 기초
(1) 네트워크 작성 기초
- 객체 선언 후 노드와 엣지 추가, 노드의 좌표를 설정해 네트워크를 그릴 수 있다.
G = nx.Graph()
G.add_node('nodeA')
G.add_node('nodeB')
G.add_node('nodeC')
G.add_edge('nodeA','nodeB')
G.add_edge('nodeA','nodeC')
G.add_edge('nodeB','nodeC')
pos={}
pos['nodeA']=(0,0)
pos['nodeB']=(1,1)
pos['nodeC']=(0,1)
nx.draw(G,pos,with_labels=True)
plt.show()

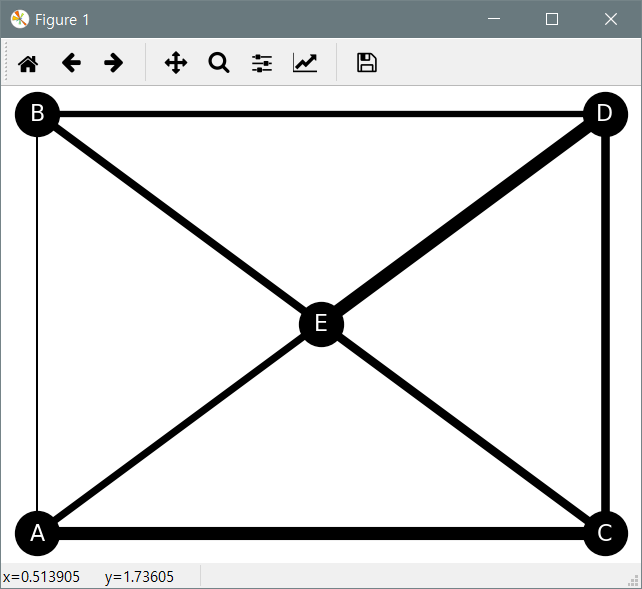
(2) 경로 가중치 부여
- 가중치를 부여해 노드 사이의 엣지 굵기를 바꾸기
- 가중치 정보 ( df_w )
- 각 엣지의 위치 ( df_p )

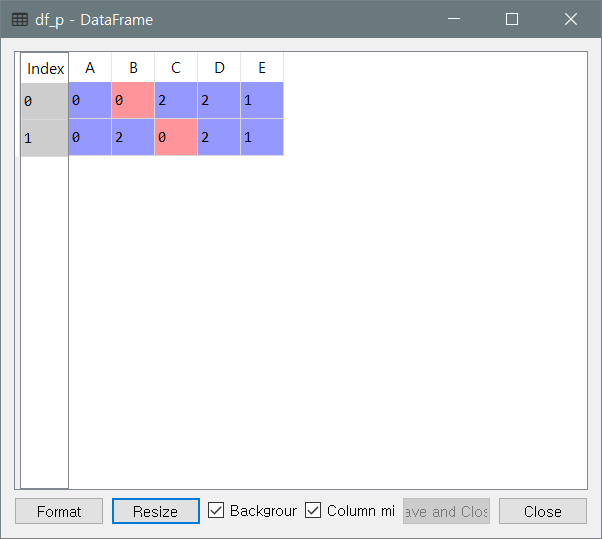
df_w = pd.read_csv('network_weight.csv')
df_p = pd.read_csv('network_pos.csv')
# 엣지 가중치 만들기
size = 10
weight = []
for i in range(len(df_w)) :
for j in range(len(df_w.columns)):
weight.append(df_w.iloc[i][j]*size)
# 노드, 엣지 추가
G = nx.Graph()
for i in range(len(df_w.columns)):
G.add_node(df_w.columns[i])
for i in range(len(df_w.columns)) :
for j in range(len(df_w.columns)):
G.add_edge(df_w.columns[i],df_w.columns[j])
# 노드 좌표 설정
pos ={}
for i in range(len(df_w.columns)):
node = df_w.columns[i]
pos[node] = (df_p[node][0],df_p[node][1])
nx.draw(G,pos,with_labels=True,font_size=16, node_size=1000, node_color='k', font_color='w',width=weight)
plt.show()
4. 공장 데이터로 운송 경로 가시화
- 어느 창고에서 어느 공장이로든 골고루 운송 경로가 있으므로 줄이는 것이 개선방향
G = nx.Graph()
# 노드 추가 7개
for i in range(len(df_pos.columns)):
G.add_node(df_pos.columns[i])
# 엣지 설정, 가중치 리스트화
num_pre = 0
edge_weights =[]
size = 0.1
for i in range(len(df_pos.columns)):
for j in range(len(df_pos.columns)):
if not (i==j):
# 엣지 추가
G.add_edge(df_pos.columns[i],df_pos.columns[j])
# 엣지 가중치 추가
if num_pre<len(G.edges):
num_pre = len(G.edges)
weight = 0
if (df_pos.columns[i] in df_tr.columns)and(df_pos.columns[j] in df_tr.index):
if df_tr[df_pos.columns[i]][df_pos.columns[j]]:
weight = df_tr[df_pos.columns[i]][df_pos.columns[j]]*size
elif(df_pos.columns[j] in df_tr.columns)and(df_pos.columns[i] in df_tr.index):
if df_tr[df_pos.columns[j]][df_pos.columns[i]]:
weight = df_tr[df_pos.columns[j]][df_pos.columns[i]]*size
edge_weights.append(weight)
# 좌표 설정
pos = {}
for i in range(len(df_pos.columns)):
node = df_pos.columns[i]
pos[node] = (df_pos[node][0],df_pos[node][1])
# 그리기
nx.draw(G, pos, with_labels=True,font_size=16, node_size = 1000, node_color='k', font_color='w', width=edge_weights)
plt.show()

5. 운송 비용 최소화하기위한 최적화
- 최적화 문제를 푸는 패턴 - 다양한 조합 중에 제약 조건을 만족시키며 목적함수를 최대, 최소화 시키는 조합 선택
(1) 최적화 하고싶은 것을 함수로 정의 - 목적함수
(2) 최적화 하기 위해 지켜야 할 조건 정의 - 제약 조건
(1) 운송 비용 함수
- 운송량과 비용 곱의 총합으로 1493만원의 총 운송비용 집계
def trans_cost(df_tr,df_tc):
cost = 0
for i in range(len(df_tc.index)):
for j in range(len(df_tr.columns)):
cost += df_tr.iloc[i][j]*df_tc.iloc[i][j]
return cost
trans_cost(df_tr,df_tc)

(2) 제약 조건
- 실제 운송량과 가능한 수요량, 공급량 비교해보기
# 수요측 제약조건
for i in range(len(df_demand.columns)):
temp_sum = sum(df_tr[df_demand.columns[i]])
print(str(df_demand.columns[i])+"실제 운송량:"+str(temp_sum)+" (수요량:"+str(df_demand.iloc[0][i])+")")
if temp_sum>=df_demand.iloc[0][i]:
print("수요량을 만족시키고있음")
else:
print("수요량을 만족시키지 못하고 있음. 운송경로 재계산 필요")
# 공급측 제약조건
for i in range(len(df_supply.columns)):
temp_sum = sum(df_tr.loc[df_supply.columns[i]])
print(str(df_supply.columns[i])+"실제 운송량:"+str(temp_sum)+" (공급 범위:"+str(df_supply.iloc[0][i])+")")
if temp_sum<=df_supply.iloc[0][i]:
print("공급 범위내")
else:
print("공급 범위 초과. 운송경로 재계산 필요")

(3) 운송경로 변경 테스트
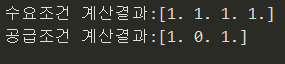
- 위의 비교문을 사용해 조건을 만족하면 1, 만족하지 않으면 0 출력하도록 함
- 비용 절감은 했으나, 공급 가능 범위를 넘어버려 실행 불가능
trans_cost(df_tr_new,df_tc)
# 수요측
def condition_demand(df_tr,df_demand):
flag = np.zeros(len(df_demand.columns))
for i in range(len(df_demand.columns)):
temp_sum = sum(df_tr[df_demand.columns[i]])
if (temp_sum>=df_demand.iloc[0][i]):
flag[i] = 1
return flag
# 공급측
def condition_supply(df_tr,df_supply):
flag = np.zeros(len(df_supply.columns))
for i in range(len(df_supply.columns)):
temp_sum = sum(df_tr.loc[df_supply.columns[i]])
if temp_sum<=df_supply.iloc[0][i]:
flag[i] = 1
return flag
print("수요조건 계산결과:"+str(condition_demand(df_tr_new,df_demand)))
print("공급조건 계산결과:"+str(condition_supply(df_tr_new,df_supply)))

+ 참고 자료 및 출처
- 책 <파이썬 데이터 분석 실무 테크닉 100>
- 데이터 github.com/wikibook/pyda100
'Analysis > Example' 카테고리의 다른 글
| 물류 네트워크 설계 - 생산 계획 (0) | 2021.02.18 |
|---|---|
| 물류 네트워크 설계 - 최적화 라이브러리 (4) | 2021.02.15 |
| 물류 데이터 분석 - 데이터 가공, 통계량 파악 (0) | 2021.02.15 |
| 스포츠센터 회원 분석 - 의사결정나무 (0) | 2021.02.07 |
| 스포츠센터 회원 분석 - 클러스터링, 회귀분석 (0) | 2021.01.30 |




댓글