정상성 (Stationarity)
- 평균, 분산, 공분산이 시간의 흐름에 따라 변하지 않음

- 약정상 - 두 변수 비교
- 𝐸(𝑋𝑡) = 𝜇 for all time 𝑡 (The first moment estimation)
- 𝑉𝑎𝑟(𝑋𝑡) = 𝐸(𝑋^2𝑡) − 𝐸(𝑋𝑡)^2 <∞ for all time 𝑡 (The second moment estimation)
- 𝐶𝑜𝑣(𝑋𝑖𝑠,𝑋𝑖𝑘) = 𝐶𝑜𝑣(𝑋𝑖(𝑠+ℎ), 𝑋𝑖(𝑘+ℎ))=𝑓(ℎ) for all time 𝑠, 𝑘, ℎ (The cross moment estimation) => covariance just depends on ℎ.
- 강정상
- 예시 - White noise
- 약정상은 두 변수로 비교했다면, 강정상은 세 변수부터 모든 변수들의 정상성을 확인함
- 비정상 확률과정
- 예시 - Random walk
- 일차모멘트, 이차모멘트가 변화

- 용어
- Stationary Process: 정상성인 시계열데이터를 발생시키는 데이터셋(프로세스)
- Stationary Model: 정상성인 시계열데이터를 설명하는 모델
- Trend Stationary: 트랜드를 제거하면 정상성인 시계열데이터
- Seasonal Stationary: 계절성을 제거하면 정상성인 시계열데이터
- Difference Stationary: 차분을하면 정상성인 시계열데이터
- Strictly Stationary: 시간 흐름에 따라 "통계적 특성"이 변하지 않음
- 비정상성 Y를 정상성으로 변환함 ( 필수 아님 )
- 안정성과 예측력 향상 - 모델이 단순해져 overfitting 감소
- 로그, 차분, Box-Cox 등
- 잔차 정상성 변환 후 통계량으로 확인
1. 로그 변환
- 시간과 비례해 분산이 커지는 경우에 적절

2. 차분(diff)
- 계절성(seasonality), 추세(trend) 효과 제거 가능
(1) 계절성 제거 방법
1. 계절성함수 추정해 제거
2. 차분으로 계절성 제거
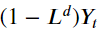
(2) 추세 제거 방법
1. 추세함수 추정해 제거
2. 차분으로 계절성 제거
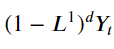
3. Box-Cox 변환
- 정규분포가 아닌 데이터를 정규분포로 변환함
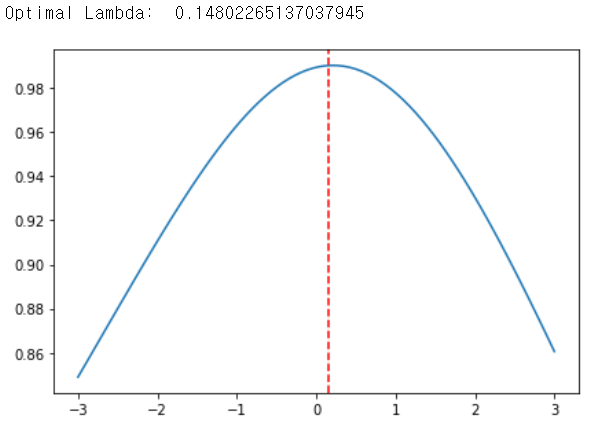
- 여러 파라미터를 넣어보고 가장 정규성을 높여주는 값을 사용
# lambda를 바꿔가며 정규성(measure:y)이 가장 높은 lambda(l_opt)를 선정
x, y = sp.stats.boxcox_normplot(raw.value, la=-3, lb=3) # -3 ~ 3 범위에서 test
y_transfer, l_opt = sp.stats.boxcox(raw.value)
print('Optimal Lambda: ', l_opt)
plt.figure(figsize=(12,4))
sm.qqplot(raw.value, fit=True, line='45', ax=plt.subplot(131))
plt.title('Y')
sm.qqplot(np.log(raw.value), fit=True, line='45', ax=plt.subplot(132))
plt.title('Log(Y)')
sm.qqplot(y_transfer, fit=True, line='45', ax=plt.subplot(133))
plt.title('BoxCox(Y)')
plt.tight_layout()
plt.show()

정상성 테스트
- 정상성 (Stationarity) : 평균, 분산, 공분산이 시간의 흐름에 따라 변하지 않음
- ADF : 추세 제거 확인 검정통계량 ( H1 : 정상 )
- KPSS : 계절성 제거 확인 검정통계량 ( H1 : 비정상 )
- ACF : 데이터에 계절성이 포함되면 ACF의 비정상 Lag 존재 가능 / 추세가 포함되면 ACF의 비정상 Lag 존재 가능
def stationarity_adf_test(Y_Data, Target_name):
if len(Target_name) == 0:
Stationarity_adf = pd.Series(sm.tsa.stattools.adfuller(Y_Data)[0:4],
index=['Test Statistics', 'p-value', 'Used Lag', 'Used Observations'])
for key, value in sm.tsa.stattools.adfuller(Y_Data)[4].items():
Stationarity_adf['Critical Value(%s)'%key] = value
Stationarity_adf['Maximum Information Criteria'] = sm.tsa.stattools.adfuller(Y_Data)[5]
Stationarity_adf = pd.DataFrame(Stationarity_adf, columns=['Stationarity_adf'])
else:
Stationarity_adf = pd.Series(sm.tsa.stattools.adfuller(Y_Data[Target_name])[0:4],
index=['Test Statistics', 'p-value', 'Used Lag', 'Used Observations'])
for key, value in sm.tsa.stattools.adfuller(Y_Data[Target_name])[4].items():
Stationarity_adf['Critical Value(%s)'%key] = value
Stationarity_adf['Maximum Information Criteria'] = sm.tsa.stattools.adfuller(Y_Data[Target_name])[5]
Stationarity_adf = pd.DataFrame(Stationarity_adf, columns=['Stationarity_adf'])
return Stationarity_adf
def stationarity_kpss_test(Y_Data, Target_name):
if len(Target_name) == 0:
Stationarity_kpss = pd.Series(sm.tsa.stattools.kpss(Y_Data)[0:3],
index=['Test Statistics', 'p-value', 'Used Lag'])
for key, value in sm.tsa.stattools.kpss(Y_Data)[3].items():
Stationarity_kpss['Critical Value(%s)'%key] = value
Stationarity_kpss = pd.DataFrame(Stationarity_kpss, columns=['Stationarity_kpss'])
else:
Stationarity_kpss = pd.Series(sm.tsa.stattools.kpss(Y_Data[Target_name])[0:3],
index=['Test Statistics', 'p-value', 'Used Lag'])
for key, value in sm.tsa.stattools.kpss(Y_Data[Target_name])[3].items():
Stationarity_kpss['Critical Value(%s)'%key] = value
Stationarity_kpss = pd.DataFrame(Stationarity_kpss, columns=['Stationarity_kpss'])
return Stationarity_kpss
display(stationarity_adf_test(result.resid, []))
display(stationarity_kpss_test(result.resid, []))
sm.graphics.tsa.plot_acf(result.resid, lags=50, use_vlines=True)

# 로그 변환
candidate_trend = np.log(raw).copy()
# 추세 차분
trend_diff_order_initial = 0
result = stationarity_adf_test(candidate_trend.values.flatten(), []).T
if result['p-value'].values.flatten() < 0.1:
trend_diff_order = trend_diff_order_initial
else:
trend_diff_order = trend_diff_order_initial + 1
candidate_seasonal = candidate_trend.diff(trend_diff_order).dropna().copy()
# 계절 차분 (acf 그래프에서 가장 높은 위치 인덱스)
seasonal_diff_order = sm.tsa.acf(candidate_seasonal)[1:].argmax() + 1 # 12
print('Seasonal Difference: ', seasonal_diff_order)
candidate_final = candidate_seasonal.diff(seasonal_diff_order).dropna().copy()



+ 참고 자료 및 출처
- 김경원 < 파이썬을 활용한 시계열 데이터 분석 A-Z 강의 > ( 패스트캠퍼스 강의 )
'Analysis > Time series' 카테고리의 다른 글
| Lecture 12. 적분 선형확률과정 (0) | 2021.04.01 |
|---|---|
| Lecture 11. 단순 선형확률과정 (0) | 2021.03.29 |
| Lecture 9. 시계열 머신러닝 알고리즘 (1) | 2021.03.27 |
| Lecture 8. 시계열 데이터 전처리 (0) | 2021.03.18 |
| Lecture 7. 잔차진단 (0) | 2021.03.16 |




댓글