Lecture 12. 적분 선형확률과정

 

 

1. ARIMA (Auto-Regressive Integrated Moving Average)

 

 

ARIMA(p,d,q)

 

추세차분

 

• 1 이상의 추세차분이 적용(d>=1)된 Yt가 AR(p)와 MA(q)의 선형조합
• Yt는 단위근 가진 비정상성, d번 차분한 Yt는 정상성 데이터
• 차분해야 정상성이 되는 Yt는 lag가 증가해도 ACF가 1에 가까워 쉽게 감소하지 않음
• c 파라미터 (상수항) : 이론 수식 복잡성으로 생략 가능
• d 파라미터 (차분) : 예측 구간추정범위를 급격히 상승, 과차분은 MA모형을 생성 -> ACF/PACF 증가

 

(1) ARIMA(0.0.0) : WN

(2) ARIMA(0,1,0) : Random Walk

(3) ARIMA(p,0,0) = AR(p) 

(4) ARIMA(0,0,q) = MA(q)

(5) p=0, ARIMA(0,d,q) = IMA(d,q)

(6) q=0, ARIMA(p,d,0) = ARI(p,d)

 

 

 

2. SARIMA (Seasonal ARIMA)

 

계절성 파트는 계절성이 나타나는 부분에만 ARMA 적용

 

 

AR(p)tr AR(p)se 추세차분 계절성차분 = MA(q)tr MA(q)se

 

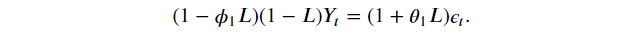
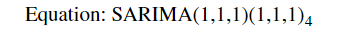
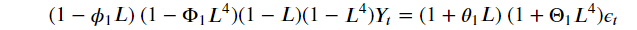
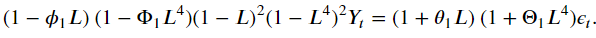
• ARIMA는 Non-seasonal 로 계절성 반영 모델 필요
• Multiplicated SARIMA(p,d,q)x(P,D,Q,m)

 

p	trend AR
d	trend difference
q	trend MA
m	time steps
P	seasonal AR
D	seasonal difference
Q	seasonal MA

 

 

 

(1) Simple SARIMA - 계절성시차에서만 ACF가 유의하지 않음

 

 

1. SARIMA(0,0,0)(0,0,1,12)

 

• ACF가 12마다 유의수준을 벗어난 증가 보임 / PACF 지수적 감소

 

SARIMA(0,0,0)(0,0,1,12) / 𝑌𝑡 = 𝜖𝑡 + Θ𝜖(𝑡−12)

 

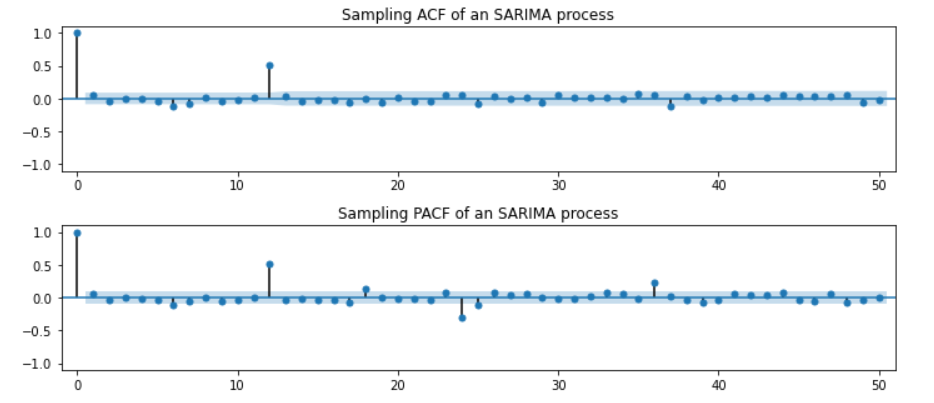
2. SARIMA(0,0,0)(1,0,0,12)

 

• ACF가 지수적 감소 / PACF가 12마다 유의수준을 벗어난 증가 보임

 

SARIMA(0,0,0)(1,0,0,12) / 𝑌𝑡 =Φ𝑌(𝑡−12) + 𝜖𝑡

 

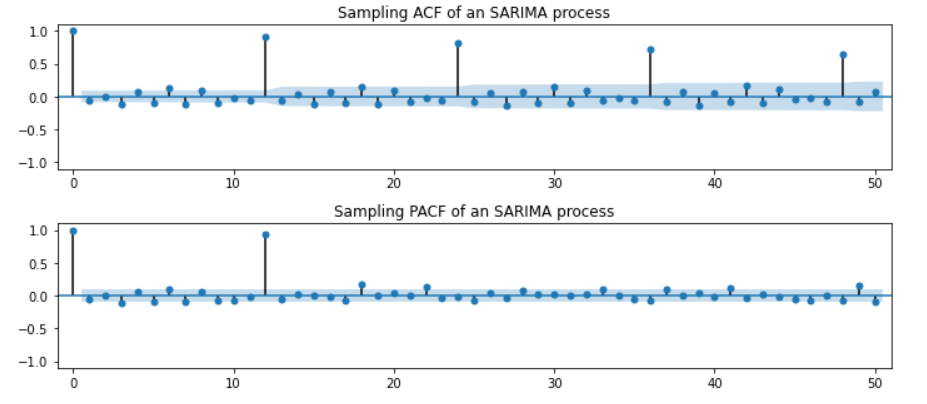
3. SARIMA(0,0,0)(0,1,1,12)

 

• 단위근으로 계절성 차분을 해야 정상화가 되는 데이터
• 12 차수마다 단위근이 들어가 ACF가 반복되는 경향을 보임
• 뒤로 갈수록 계절성을 잡아내지 못해 PACF가 unstable

 

SARIMA(0,0,0)(0,1,1,12) / 𝑌𝑡 = 𝑌(𝑡−12) + 𝜖𝑡 + Θ1𝜖(𝑡−12)

 

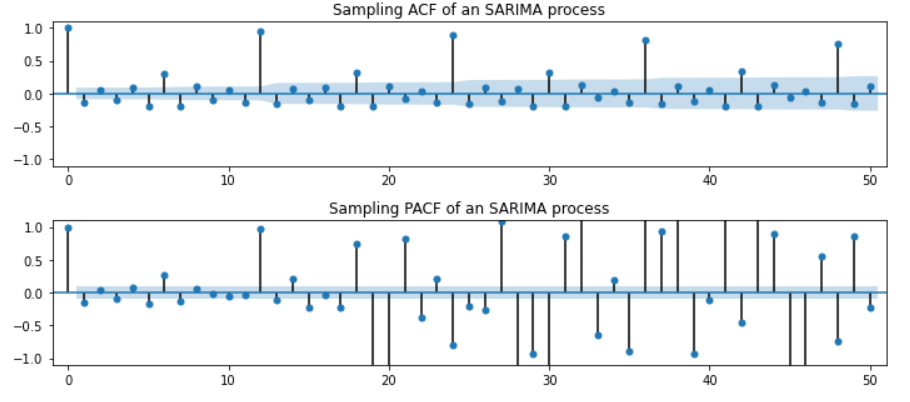
4.  SARIMA(0,0,0)(1,1,0,12)

 

• 계절성 차분을 해야 정상화가 되는 데이터
• 수치가 작아졌다 커지는 불규칙하게 진동하는 듯한 ACF

 

𝑌𝑡 = (1+Φ1)𝑌(𝑡−12) − Φ1𝑌(𝑡−24) + 𝜖𝑡

 

 

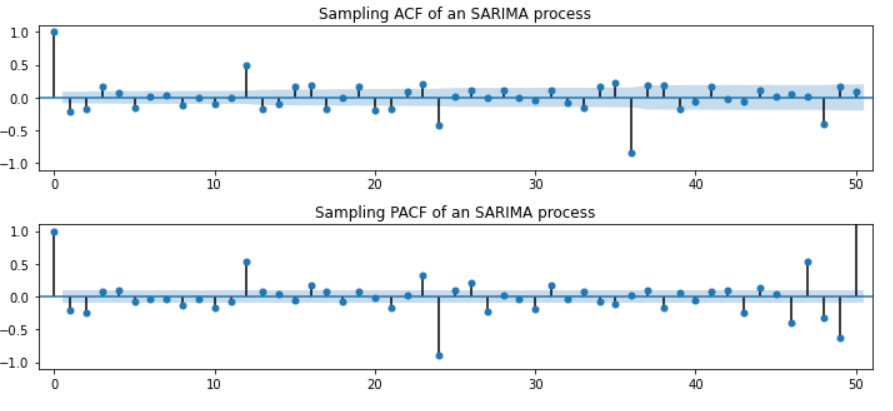
(2) Multiplicated SARIMA - 계절성시차와 그 주변시차도 ACF가 유의하지 않음

 

 

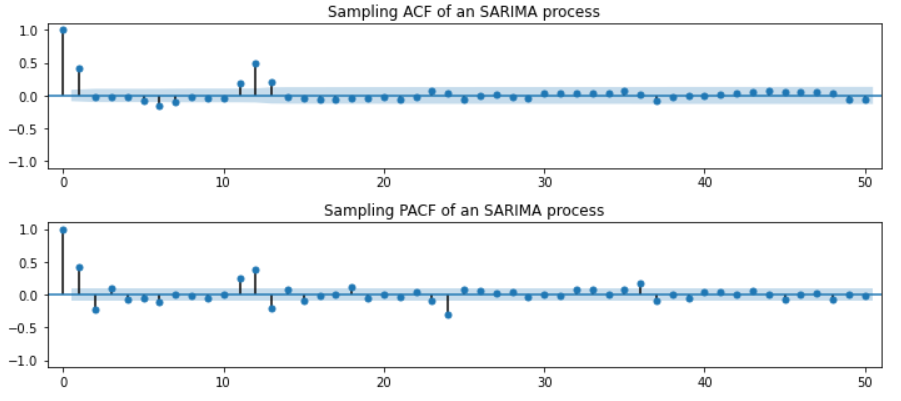
1. SARIMA(0,0,1)(0,0,1,12)

 

• 계절주기 12고 계절주기 자료들 간에는 ARIMA(0,0,1), 비계절 자료들 간에는 ARIMA(0,0,1)
• 시차(Lag)가 1, 11, 12, 13인 경우를 제외하고는 자기상관계수가 모두 0

 

𝑌𝑡 = 𝜖𝑡 + 𝜃𝜖(𝑡−1) + Θ𝜖(𝑡−12) + 𝜃Θ𝜖(𝑡−13)

 

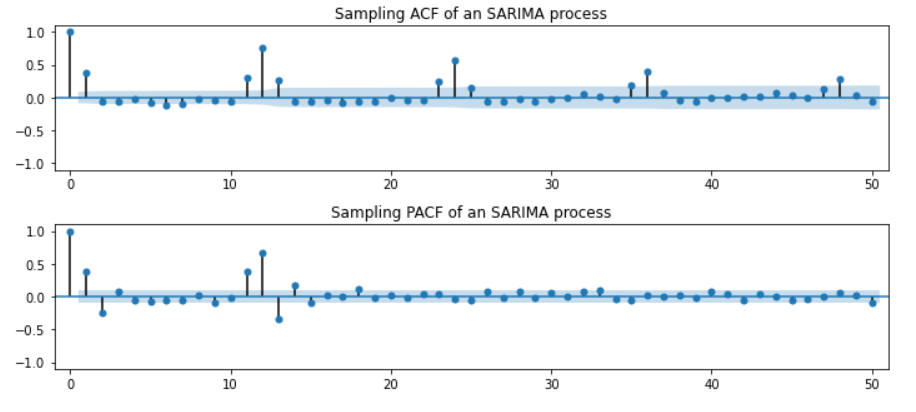
2. SARIMA(0,0,1)(1,0,0,12)

 

• 계절주기 12고 계절주기 자료들 간에는 ARIMA(1,0,0), 비계절 자료들 간에는 ARIMA(0,0,1)
• 시차(Lag)가 12의 배수와 그 앞/뒤인 경우(12𝑘, 12𝑘+1, 12𝑘-1)를 제외하고는 자기상관계수가 모두 0

 

𝑌𝑡 = Φ𝑌(𝑡−12)+𝜖𝑡+𝜃𝜖(𝑡−1)

 

3. SARIMA(0,1,0)(0,1,0,12)

 

• 계절주기 12고 계절주기 간 1차 차분 ARIMA(0,1,0), 비계절 자료들 간 1차 차분 ARIMA(0,1,0
• 시계열을 1차 차분하고 그 시계열을 다시 12간격 차분하면 백색잡음
• 𝑌𝑡 = 𝑌(𝑡−1)+𝑌(𝑡−12)−𝑌(𝑡−13)+𝜖𝑡

 

4. SARIMA(0,1,1)(0,1,1,12)

 

• 계절주기 12고 계절/비계절 자료 모두 1차 차분 ARIMA(0,1,1)
• 시계열을 1차 차분하고 그 시계열을 다시 12간격 차분하면 계절/비계절 자료 모두 ARIMA(0,0,1)
• 𝑌𝑡 = 𝑌(𝑡−1)+𝑌(𝑡−12)−𝑌(𝑡−13)+𝜖𝑡+𝜃𝜖(𝑡−1)+Θ𝜖(𝑡−12)+𝜃Θ𝜖(𝑡−13)

 

5. SARIMA(1,1,0)(1,1,0,12)

 

• 계절주기 12고 계절/비계절 자료 모두 1차 차분 ARIMA(1,1,0)
• 시계열을 1차 차분하고 그 시계열을 다시 12간격 차분하면 계절/비계절 자료 모두 ARIMA(1,0,0)
• 𝑌𝑡−(1+𝜙)𝑌(𝑡−1)+𝜙𝑌(𝑡−2)−(1+Φ)𝑌(𝑡−12)+((1+Φ)+𝜙(1+Φ))𝑌(𝑡−13)−𝜙(1+Φ)𝑌(𝑡−14)+Φ𝑌(𝑡−24)−(Φ+𝜙Φ)𝑌(𝑡−25)+𝜙Φ𝑌(𝑡−26) = 𝜖𝑡

 

 

 

+ 참고 자료 및 출처

 

• 김경원 < 파이썬을 활용한 시계열 데이터 분석 A-Z  강의 >  ( 패스트캠퍼스 강의 )