- 일반 선형확률과정
- 시계열 데이터가 가우시안 백색잡음의 현재값과 과거값의 선형조합

- WN, MA, AR, ARMA, ARIMA, SARIMA
1. WN (White Noise)
- 잔차들은 정규분포, 평균 0, 일정한 분산, 가져야 함
- 시간의 흐름에 따라 상관성이 없어야 함 (cov = 0, autocorrelation = 0) : ACF로 확인
- 강정상 과정의 대표적 예시
- 가우시안 백색잡음, 베르누이 백색잡음
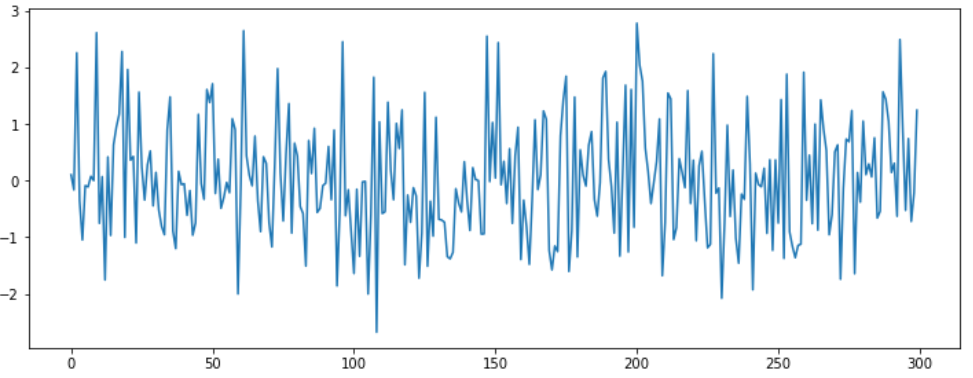

2. MA (Moving Average)
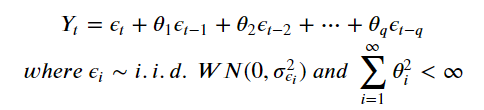
- 차수가 유한한 (q) 가우시안 백색잡음의 선형조합
- Trend-cycle
- ACF가 q+1항부터 0으로 수렴
- PACF가 지수적 감소, 진동하는 사인 형태
# ARMA(0,1) = MA(1)
ar_params = np.array([]) #0
ma_params = np.array([0.65])
ar, ma = np.r_[1, -ar_params], np.r_[1, ma_params]
ar_order, ma_order = len(ar)-1, len(ma)-1
y = statsmodels.tsa.arima_process.arma_generate_sample(ar, ma, nsample=1000, burnin=500)
fit = statsmodels.tsa.arima_model.ARMA(y, (ar_order,ma_order)).fit(trend='c', disp=0)
pred_ts_point = fit.forecast(steps=ahead)[0] # 점추정
pred_ts_interval = fit.forecast(steps=ahead)[2] # 구간추정
display(fit.summary2())
plt.figure(figsize=(12,3))
statsmodels.graphics.tsaplots.plot_acf(y, lags=50, zero=True, use_vlines=True, alpha=0.05, ax=plt.subplot(121))
statsmodels.graphics.tsaplots.plot_pacf(y, lags=50, zero=True, use_vlines=True, alpha=0.05, ax=plt.subplot(122))
plt.show()
3. AR (Auto-Regressive)
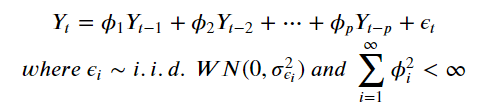
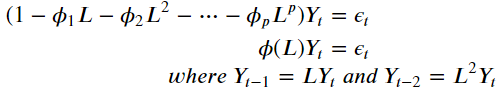
- 차수가 유한한 (p) 자기자신의 과거값들의 선형조합
- PACF가 p+1항부터 0으로 수렴
- ACF가 지수적 감소, 진동하는 사인 형태
- AR(1) : 𝜙1=1 은 랜덤워크 (𝑌𝑡 = 𝑌𝑡-1 + 𝜖𝑡)
# ARMA(1,0) = AR(1)
ar_params = np.array([0.75])
ma_params = np.array([]) #0
ar, ma = np.r_[1, -ar_params], np.r_[1, ma_params]
ar_order, ma_order = len(ar)-1, len(ma)-1
y = statsmodels.tsa.arima_process.arma_generate_sample(ar, ma, nsample=1000, burnin=500)
fit = statsmodels.tsa.arima_model.ARMA(y, (ar_order,ma_order)).fit(trend='c', disp=0)
pred_ts_point = fit.forecast(steps=ahead)[0] # 점추정
pred_ts_interval = fit.forecast(steps=ahead)[2] # 구간 추정
display(fit.summary2())
plt.figure(figsize=(12,3))
statsmodels.graphics.tsaplots.plot_acf(y, lags=50, zero=True, use_vlines=True, alpha=0.05, ax=plt.subplot(121))
statsmodels.graphics.tsaplots.plot_pacf(y, lags=50, zero=True, use_vlines=True, alpha=0.05, ax=plt.subplot(122))
plt.show()
+ MA와 AR의 가역성 조건 (Invertibility Condition)
(1) MA(q) -> AR(∞) : 변환 후에 AR이 정상성이면 Invertibility
(2) AR(p) -> MA(∞) : 변환 후에 MA가 invertibility를 만족하는 건 1개 모형뿐
4. ARMA (Auto-Regressive Moving Average)
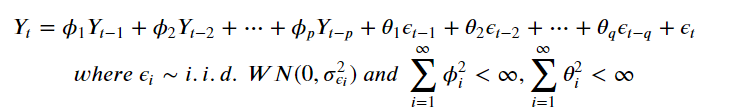
- ARMA(p,q) : AR(p)와 MA(q)의 선형조합
- 데이터를 정상성 형태로 변환시켜 ACF, PACF로 차수 추론
- ACF가 q+1항부터 지수적 감소, 진동하는 사인 형태
- PACF가 p+1항부터 지수적 감소, 진동하는 사인 형태
- ARMA는 추세를 제거하는 것이 목적 - 계절성 제거 X
# ARMA(1,1)
ar_params = np.array([0.75])
ma_params = np.array([0.65])
ar, ma = np.r_[1, -ar_params], np.r_[1, ma_params]
ar_order, ma_order = len(ar)-1, len(ma)-1
y = statsmodels.tsa.arima_process.arma_generate_sample(ar, ma, nsample=1000, burnin=500)
fit = statsmodels.tsa.arima_model.ARMA(y, (ar_order,ma_order)).fit(trend='c', disp=0)
pred_ts_point = fit.forecast(steps=ahead)[0]
pred_ts_interval = fit.forecast(steps=ahead)[2]
display(fit.summary2())
plt.figure(figsize=(12,3))
statsmodels.graphics.tsaplots.plot_acf(y, lags=50, zero=True, use_vlines=True, alpha=0.05, ax=plt.subplot(121))
statsmodels.graphics.tsaplots.plot_pacf(y, lags=50, zero=True, use_vlines=True, alpha=0.05, ax=plt.subplot(122))
plt.show()
5. ARMAX (ARMA with eXogenous)

fit = sm.tsa.ARMA(raw_using.consump, (1,1), exog=raw_using.m2).fit()
display(fit.summary())
+ 참고 자료 및 출처
- 김경원 < 파이썬을 활용한 시계열 데이터 분석 A-Z 강의 > ( 패스트캠퍼스 강의 )
'Analysis > Time series' 카테고리의 다른 글
| Lecture 13. 선형확률과정 분석실습 (0) | 2021.04.03 |
|---|---|
| Lecture 12. 적분 선형확률과정 (0) | 2021.04.01 |
| Lecture 10. 타겟 데이터 정상성 변환 (0) | 2021.03.27 |
| Lecture 9. 시계열 머신러닝 알고리즘 (1) | 2021.03.27 |
| Lecture 8. 시계열 데이터 전처리 (0) | 2021.03.18 |




댓글