선형확률과정 분석 사이클
- 3~5단계 자동화
1. 데이터 전처리 및 시각화를 통해 Outlier 확인/변경/제거
2. 비정상 과정에서 정상 과정 추출 - 결정론적 추세나 확률적 추세가 있는지 확인
- 결정론적 추세는 회귀분석, 다항식 등으로 모형화 후 이를 분리
- 확률적 추세(ARIMA 모형) 경우에는 ADF(Augmented Dickey Fuller) 검정을 사용하여 적분차수로 차분
3. 정규성 확인 - 정규성 검정을 통해 자료의 분포가 정규 분포인지 확인
- 일반 선형 확률 과정인 경우에는 전체 시계열이 가우시안 백색 잡음의 선형 조합으로 이루어지기 때문에 시계열 자체도 가우시안 정규 분포
- ARIMA 모형 등의 일반 선형 확률 과정으로 모형화하려면 우선 정규성 검정(Normality Test)을 사용하여 분포가 정규 분포인지 확인
- 만약 시계열 자료의 분포가 로그 변환이나 Box-Cox 변환을 사용하여 정규성이 개선된다면 이러한 변환을 사용 가능
4. 정상 과정에 대한 ARMA 모형 차수 결정 - ACF/PACF 분석으로 AR(p) 모형 또는 MA(q) 모형 결정
- ACF가 특정 차수 이상에서 없어지는 경우(Cut-off)에는 MA 모형을 사용 가능
- PACF가 특정 차수 이상에서 없어지면 AR 모형을 사용 가능
- ACF와 PACF 모두 특정 차수 이상에서 없어지는 현상이 나타나지 않는다면 ARMA 모형을 사용
- ARMA 모형인 경우 모수 추정시 AIC/BIC 값을 이용하여 차수 결정 및 모수추정도 동시에 이루어 짐
5. ARMA 모형의 모수 추정
- MM(Method of Modent)/LS(Least Square)/MLE(Maximum Likelihood Estimation) 등의 방법론으로 모수 추정
- ADF(Augmented Dickey Fuller) 검정을 사용하여 해당 수식에 대한 계수 즉 모수 값을 추정
- 부트스트래핑을 사용하여 모수의 표준 오차 추정
6. 잔차 진단 (모형 진단)
- 모형이 추정된 잔차 진단 과정을 통해 추정이 올바르게 이루어졌는지 검증
- 기본적으로 잔차(Residual)가 백색 잡음이 되어야 함
- 잔차에 대한 정규성 검정
- 잔차에 대한 ACF 분석 또는 Ljung-Box Q 검정으로 모형 차수 재확인
- 잔차가 백색잡음이 아니면 새로운 모형으로 모든 단계(1~5단계)를 새로 시작
- 잔차가 백색잡음이면 일단은 예측력을 확인 -> 예측력이 낮을 시 새로운 모형으로 모든 단계(1~5단계)를 새로 시작
항공사 고객수요 간단한 실습 코드
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
%reload_ext autoreload
%autoreload 2
from module import stationarity_adf_test, stationarity_kpss_test
data = sm.datasets.get_rdataset("AirPassengers")
raw = data.data.copy()
# 1. 데이터 전처리
# 시간 인덱싱
if 'time' in raw.columns:
raw.index = pd.date_range(start='1/1/1949', periods=len(raw['time']), freq='M')
del raw['time']
# 2. 정상성 확인
candidate_none = raw.copy()
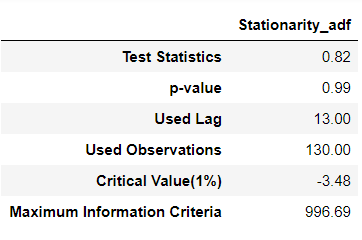
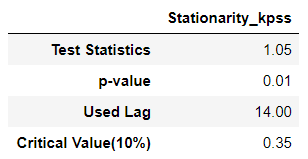
display(stationarity_adf_test(candidate_none.values.flatten(), []))
display(stationarity_kpss_test(candidate_none.values.flatten(), []))
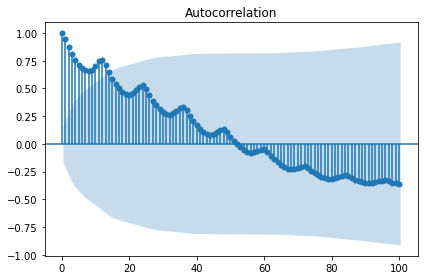
sm.graphics.tsa.plot_acf(candidate_none, lags=100, use_vlines=True)
plt.tight_layout()
plt.show()
# 3. 정규성 확인
# 로그 변환
candidate_trend = np.log(raw).copy()
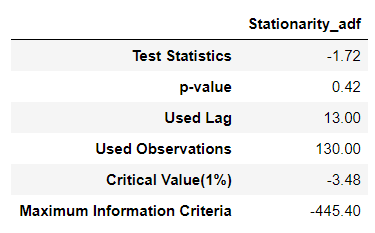
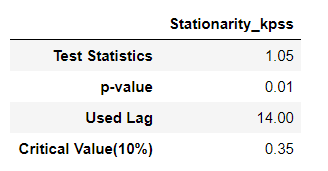
display(stationarity_adf_test(candidate_trend.values.flatten(), []))
display(stationarity_kpss_test(candidate_trend.values.flatten(), []))
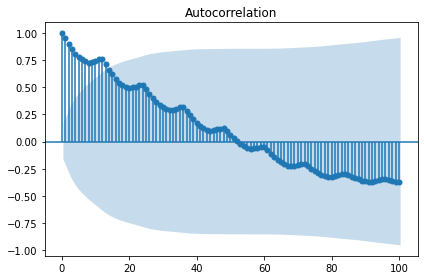
sm.graphics.tsa.plot_acf(candidate_trend, lags=100, use_vlines=True)
plt.tight_layout()
plt.show()
# 4. 차수 결정
# 로그+추세차분 변환
trend_diff_order_initial = 0
result = stationarity_adf_test(candidate_trend.values.flatten(), []).T
if result['p-value'].values.flatten() < 0.1:
trend_diff_order = trend_diff_order_initial
else:
trend_diff_order = trend_diff_order_initial + 1
print('Trend Difference: ', trend_diff_order)
candidate_seasonal = candidate_trend.diff(trend_diff_order).dropna().copy()
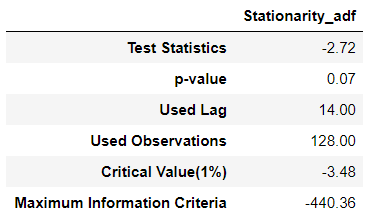
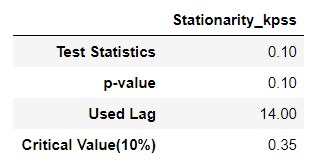
display(stationarity_adf_test(candidate_seasonal.values.flatten(), []))
display(stationarity_kpss_test(candidate_seasonal.values.flatten(), []))
sm.graphics.tsa.plot_acf(candidate_seasonal, lags=100, use_vlines=True)
plt.tight_layout()
plt.show()
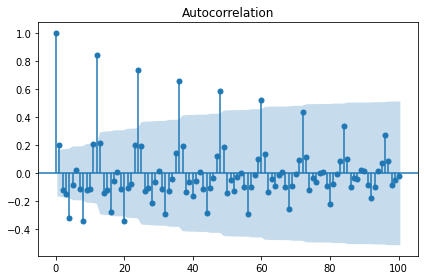
# 로그+추세차분+계절차분 변환
seasonal_diff_order = sm.tsa.acf(candidate_seasonal)[1:].argmax() + 1
print('Seasonal Difference: ', seasonal_diff_order) #12
candidate_final = candidate_seasonal.diff(seasonal_diff_order).dropna().copy()
display(stationarity_adf_test(candidate_final.values.flatten(), []))
display(stationarity_kpss_test(candidate_final.values.flatten(), []))
sm.graphics.tsa.plot_acf(candidate_final, lags=100, use_vlines=True)
plt.tight_layout()
plt.show()
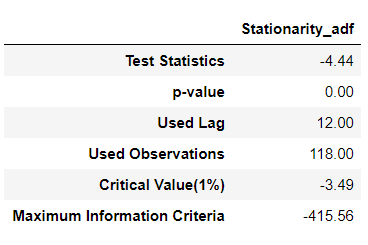
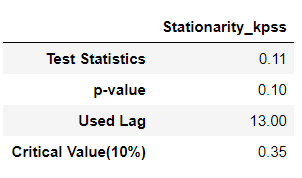
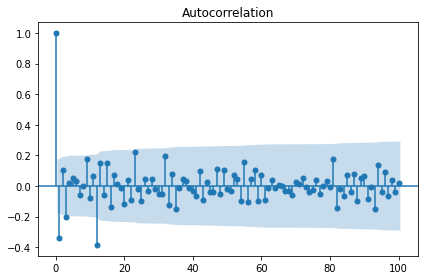
+ 참고 자료 및 출처
- 김경원 < 파이썬을 활용한 시계열 데이터 분석 A-Z 강의 > ( 패스트캠퍼스 강의 )
'Analysis > Time series' 카테고리의 다른 글
| Lecture 15. Kaggle 자전거 수요 예측 (SARIMAX / Auto-ARIMA) (0) | 2021.04.05 |
|---|---|
| Lecture 14. Kaggle 자전거 수요 예측 (RF/SARIMA) (0) | 2021.04.03 |
| Lecture 12. 적분 선형확률과정 (0) | 2021.04.01 |
| Lecture 11. 단순 선형확률과정 (0) | 2021.03.29 |
| Lecture 10. 타겟 데이터 정상성 변환 (0) | 2021.03.27 |




댓글